Embarking on the exploration of solving systems of elimination worksheet, this comprehensive guide delves into the intricacies of this fundamental algebraic technique. Designed to empower learners with a thorough understanding of the concepts and applications of elimination, this worksheet serves as an invaluable resource for students seeking to excel in their mathematical endeavors.
Delving into the nuances of elimination methods, the worksheet elucidates the step-by-step process of solving systems of equations using substitution or elimination. Through a series of carefully crafted examples, learners will gain a deep comprehension of how to manipulate equations, identify variables, and arrive at accurate solutions.
Methods for Solving Systems of Elimination
Solving systems of elimination involves finding the values of variables that satisfy a set of equations. Two common methods are substitution and elimination:
Substitution Method
Substitute the value of one variable from one equation into another equation to solve for the other variable. Repeat this process until all variables are solved.
Example:Solve the system x + y = 5, x – y = 1 using substitution.
Elimination Method
Multiply the equations by constants to make the coefficients of one variable the same. Then, add or subtract the equations to eliminate one variable and solve for the other.
Example:Solve the system 2x + 3y = 11, x – y = 2 using elimination.
Types of Elimination Problems
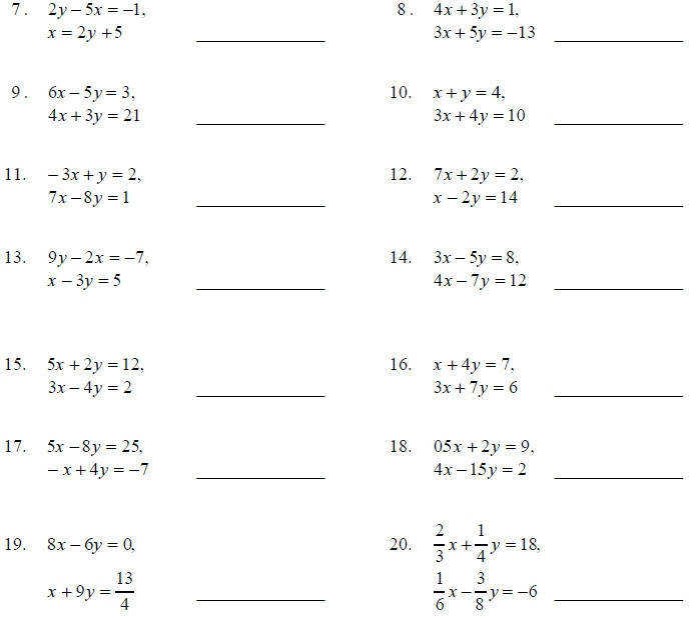
Elimination problems can be classified into three types:
Inconsistent Systems
Systems with no solution because the equations represent parallel lines or intersecting lines with different slopes.
Dependent Systems
Systems with infinitely many solutions because the equations represent the same line.
Systems with Infinite Solutions
Systems with infinitely many solutions because the equations are dependent and represent a line.
Determining the type of system is crucial to finding a valid solution.
Applications of Elimination in Real-World Scenarios
Systems of elimination are used in various fields to solve real-world problems:
Finance, Solving systems of elimination worksheet
Calculating interest rates, loan payments, and investment returns.
Engineering
Designing structures, analyzing forces, and solving circuit problems.
Science
Predicting chemical reactions, determining concentrations, and solving motion problems.
Strategies for Solving Complex Systems: Solving Systems Of Elimination Worksheet
For complex systems with multiple variables or higher degrees:
Simplify the System
Eliminate unnecessary variables or simplify equations to reduce the number of unknowns.
Use Matrices
Represent the system as a matrix and use matrix operations to solve for the variables.
Gaussian Elimination
A systematic method for transforming a system into an upper triangular form, making it easier to solve.
Using Technology to Solve Systems
Graphing calculators and online tools can assist in solving systems of elimination:
Advantages
Quick and efficient for large or complex systems.
Limitations
May not provide exact solutions or handle non-linear systems effectively.
General Inquiries
What are the different types of elimination problems?
Elimination problems can be categorized as inconsistent systems (no solution), dependent systems (infinite solutions), and systems with unique solutions.
How can I determine the type of elimination system I am dealing with?
Examine the coefficients of the variables in the equations. If any row or column contains all zeros, the system is either inconsistent or dependent.
What are some strategies for solving complex systems of elimination?
Break down the system into smaller subsystems, use substitution to eliminate variables, and employ matrices or technology for larger systems.
